En muchos casos el circuito eléctrico por donde circula la corriente no es un simple conductor sino que presenta ramificaciones o derivaciones.
El punto donde concurren mas de dos conductores se denomina “nudo” y al conjunto “red de conductores”.
En general la red de conductores puede ser muy compleja y en ella pueden encontrarse varias fuentes de tensión: baterías o generadores.
El problema consiste en determinar la intensidad de corriente de cada uno de los conductores de la red, conocidas las resistencias y las diferencias de potencial aplicadas. Este problema se resuelve aplicando la Ley de Kirchoff que se plantea a continuación:
Primera Ley de Kirchoff
La primera ley se refiere a los nudos eléctricos de un circuito y enuncia lo siguiente:
En todo nudo de una red, la suma de las corrientes que entran en él es igual a la suma de las corrientes que salen de él.
Ejemplo:
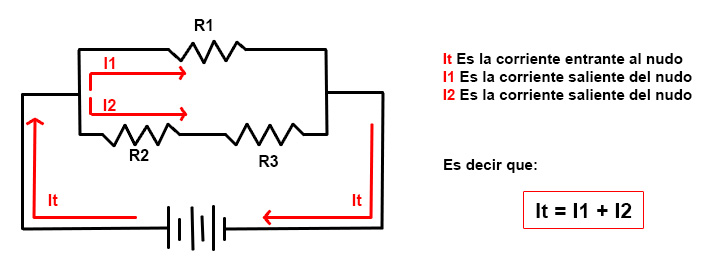
Si a la expresión en la imagen la igualamos a cero nos quedaría que: It-I1-I2 = 0
Queda evidenciado que “La suma algebraica de las corrientes que concurren a un nudo es igual a 0”
Para poder formar esta suma algebraica se antepone un signo + a las corrientes que llegan a el y un signo – a las que salen de el. Veamos otro ejemplo:
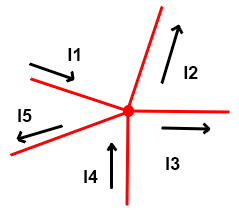
En la imagen anterior tenemos cinco corrientes y la expresión quedaría así: I1 + I4 – I2 – I3 – I5 = 0.
Lo visto se puede sintetizar con la expresión matemática:
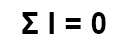
Lo que significa que la sumatoria algebraica de las corrientes es igual a cero. La letra griega para simbolizar sumatoria es Sigma mayúscula.
Segunda Ley de Kirchoff
Esta ley enuncia que “en un circuito cerrado (malla) la suma algebraica de las diferencias de potencial aplicadas es igual a la suma algebraica de las caídas de potencial”.

Veamos el siguiente ejemplo:
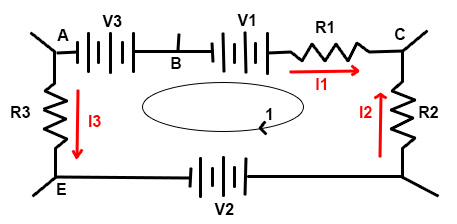
De acuerdo a la segunda Ley de Kirchoff adoptamos un sentido de circuilación de la malla, que en nuestro caso será sentido horario, como indica el número 1 en la imagen.
De esta forma obtendremos la siguiente ecuación: U3 + U1 – U2 = I1 . R1 – I2 . R2 – I3 . R3
Como vemos en el primer miembro de la igualdad se escribe la suma algebraica de las fuerzas electromotrices que aparecen al recorrer la malla en el sentido adoptado, escribiendo con signo mas (+) cuando al recorrerla nos encontramos con el polo negativo de la fuente y con signo menos (-) si al recorrerlo nos encontramos con el polo positivo de la fuente.
En el segundo miembro de la igualdad se escribe la suma algebraica de las caídas de potencial, escribiendo con signo mas (+) a aquellas caídas producidas por una corriente cuyo sentido de circulación coincide con el adoptado para recorrer la malla (en este caso sentido horario) y con un signo menos (-) cuando la caída de tensión que se produce en la resistencia da una circulación de corriente contraria al sentido adoptado.




